【統計準1級】2変量・多変量正規分布の密度関数、条件付き期待値

統計検定2級から準1級にステップアップするとき、2変量・多変量正規分布を見ただけで嫌になってしまった記憶があります。
ただし覚えることは意外と少なく、頻出といえる和(差)の分布や、条件付き期待値・分散さえ抑えておけば、大半の内容はカバーできると思います。
本記事では、まずはイメージしやすい2変量正規分布における確率密度関数と条件付き期待値・分散を例題付きで解説し、その後に多変量正規分布に拡張していきます。
まずは2変量正規分布で説明
2変量正規分布のイメージ
イメージをしやすいように、高校の期末テストを例に考えてみます。
数学\((x)\)と物理\((y)\)のテストを行ったとし、それぞれの点数が以下の正規分布に従うとします。
- 確率変数:\(\boldsymbol{X} = \begin{pmatrix} x \\ y \end{pmatrix}\)
- 平均:\(\boldsymbol{\mu}=\begin{pmatrix}\mu_X\\\mu_Y\end{pmatrix}=\begin{pmatrix}70\\50\end{pmatrix}\)
- 分散共分散:
\(\boldsymbol{\Sigma}=\begin{pmatrix}\sigma_X^2&\sigma_{XY}\\\sigma_{XY}&\sigma_Y^2\end{pmatrix}=\begin{pmatrix}10^2&9^2\\9^2&12^2\end{pmatrix}\)
2級(3級?)の内容ですが、相関係数を計算しておきます。
\[\rho=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}=\frac{9^2}{10 \times 12}=0.675\]
この設定における点数分布は以下のようになります。

\(\rho=0.675\)となるように設定したので、中程度の正の相関が見られます。
数学・物理のそれぞれは1次元正規分布に従っていますが、相関(共分散)があるため相互に影響していることを考慮する必要があります。
ちなみに、\(\rho=0\)の場合は独立になるため、それぞれの科目の正規分布のみで点数が決まります。

互いに影響することがないので、その分布は楕円のようになることは感覚的に分かると思います。
確率密度関数
先に進んででしまいますが、まずは\(k\)次元の多変量正規分布の確率密度関数をみてみます。
\[f(\boldsymbol{x})=\frac{1}{(2\pi)^{k/2}|\boldsymbol{\Sigma}|^{1/2}} \exp\!\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathsf{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right)\]
2変量正規分布の場合は\(k=2\)なので
\[ f(\boldsymbol{x}) = \frac{1}{2\pi |\Sigma|^{1/2}} \exp\!\left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right)\\ = \frac{1}{2\pi |\Sigma|^{1/2}} \exp\!\left( -\frac{1}{2} \begin{pmatrix} x-\mu_X \\[4pt] y-\mu_Y \end{pmatrix}^\top \Sigma^{-1} \begin{pmatrix} x-\mu_X \\[4pt] y-\mu_Y \end{pmatrix} \right) \]
となります。2級からステップアップしたばかりだと嫌になりそうですが、普通の1次元正規分布と照らし合わせると分かりやすいです。
1次元の正規分布の場合、行列表記ではなくなるため
\[\boldsymbol{x}=x, \boldsymbol{\mu}=\mu, \boldsymbol{\Sigma}=\sigma^2\]
となり、多変量正規分布の式に\(k=1\)を代入すると
\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}} \exp\!\left(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\right)\]見慣れた式になりました。
先ほどの数学と物理のテストの例(2変量)に戻り、平均、分散・共分散を代入してみます。
\begin{align} f(\boldsymbol{x}) &= \frac{1}{2\pi |\Sigma|^{1/2}} \exp\!\left( -\frac{1}{2} \begin{pmatrix} x-\mu_X \\[4pt] y-\mu_Y \end{pmatrix}^\top \Sigma^{-1} \begin{pmatrix} x-\mu_X \\[4pt] y-\mu_Y \end{pmatrix} \right) \\ &= \frac{1}{2\pi \sqrt{|\Sigma|}} \exp\!\left( -\frac{1}{2} \begin{pmatrix} x-70 \\[4pt] y-50 \end{pmatrix}^\top \left( \begin{matrix} 10^2 & 9^2 \\[4pt] 9^2 & 12^2 \end{matrix} \right)^{-1} \begin{pmatrix} x-70 \\[4pt] y-50 \end{pmatrix} \right) \\ &= \frac{1}{2\pi \sqrt{7839}} \exp\!\left( -\frac{1}{2} \begin{pmatrix} x-70 \\[4pt] y-50 \end{pmatrix}^\top \left( \frac{1}{7839} \begin{pmatrix} 144 & -81 \\[4pt] -81 & 100 \end{pmatrix} \right) \begin{pmatrix} x-70 \\[4pt] y-50 \end{pmatrix} \right) \end{align}
補足:\(\Sigma\)の行列式と逆行列
高校数学の範囲ですが、\(\Sigma\)の行列式\(|\Sigma|\)と、逆行列\(\Sigma^{-1}\)の計算方法を確認しておきます。
\[ \Sigma =\begin{pmatrix}a & b \\c & d\end{pmatrix} \]
に対して、行列式は
\[ |\Sigma| = ad - bc \]
となります。また、逆行列は行列式が0でないときに定義され、
\[ \Sigma^{-1} = \frac{1}{|\Sigma|} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \]
となります。
せっかくなので、数学が80点、物理が50点だった場合の確率密度を計算してみます。
\begin{align} &f(80,50)\\ &= \frac{1}{2\pi \sqrt{7839}} \exp\!\left( -\frac{1}{2} \begin{pmatrix} 80-70 \\ 50-50 \end{pmatrix}^\top \begin{pmatrix} 10^2 & 9^2 \\ 9^2 & 12^2 \end{pmatrix}^{-1} \begin{pmatrix} 80-70 \\ 50-50 \end{pmatrix} \right) \\ &= \frac{1}{2\pi \sqrt{7839}} \exp\!\left( -\frac{1}{2} \left( 10\ 0 \right) \begin{pmatrix} 100 & 81 \\ 81 & 144 \end{pmatrix}^{-1} \begin{pmatrix} 10 \\ 0 \end{pmatrix} \right) \\ &\approx 0.000719 \end{align}
と計算することができました。
例題
先ほどの数学・物理のテストの例で、頻出の内容を押さえておきます。
和・差の分布
問
数学と物理の点数の和・差が従う分布、期待値・分散を求めよ。
こちらは2級の内容なので比較的簡単ですが、本番焦らないように念のため確認しておきます。
まず、「正規分布の再生性」より、和の分布も正規分布となります。
期待値は線型なので
\[ E[X+Y] = E[X] + E[Y] = 70 + 50 = 120 \]
分散は単純な足し算ではなく、共分散が関わってきます。
\[ \mathrm{V}(X+Y) = \mathrm{V}(X) + \mathrm{V}(Y) + 2\,\mathrm{Cov}(X,Y) = 20^2 + 15^2 + 2 \times 12^2 = 913 \]
これだけです。同様に、差の期待値・分散は以下のようになります。
\[ E[X-Y] = E[X] - E[Y] = 70 - 50 = 20 \]
\[ \mathrm{V}(X-Y) = \mathrm{V}(X) + \mathrm{V}(Y) - 2\,\mathrm{Cov}(X,Y) = 20^2 + 15^2 - 2 \times 12^2 = 337 \]
条件付き期待値・分散
問
数学のテストが80点\((x=80)\)だった生徒の、物理の点数\((y)\)の条件付き期待値・分散を求めよ。
数学と物理の点数は正の相関があり、かつ数学の点数が平均点(70点)よりも高いため、物理の点数も平均点(50点)よりも高くなることは予測できます。

点数分布を見てみると、物理の点数の条件付き期待値は何となく60点前後になりそうな気がします。
ここでは導出は置いといて、2変量正規分布の条件付き期待値・分散の公式を紹介します。
条件付き期待値は頻出で、導出に時間がかかるため、こちらは公式として覚えた方が良いです。
\[ E[Y \mid X = x] = \mu_Y + \frac{\sigma_{XY}}{\sigma_X^2}(x - \mu_X) \]
\[ V[Y \mid X = x] = \sigma_Y^2 - \frac{\sigma_{XY}^2}{\sigma_X^2} \]
条件付き分散は\(x\)の値にはよらないものの、もとの分散\(\sigma_Y^2\)よりは大きくならないことが分かります。
この公式より、
\[ E[Y \mid X = 80] = 50 + \frac{81}{100}(80 - 70) = 58.1 \]
\[ V[Y \mid X = 80] = 144 - \frac{81^2}{100} = 78.39 \]
と計算できました。ちなみに、この公式は\(\sigma_{XY}=\rho\sigma_X\sigma_Y\)を使って以下のような表現を見ることもあります。
\[ E[Y \mid X = x] = \mu_Y + \rho \,\sigma_Y \frac{(x - \mu_X)}{\sigma_X} \]
\[ V[Y \mid X = x] = \sigma_Y^2 (1 - \rho^2) \]
こちらもすっきりとした形に見えます。ただし、個人的には先に示した形で覚えることをおすすめします。
理由は多変量正規分布の条件付き期待値・分散と照らし合わせることができるためです。
とはいっても、いきなりこの公式を覚えることは難しいと思います。
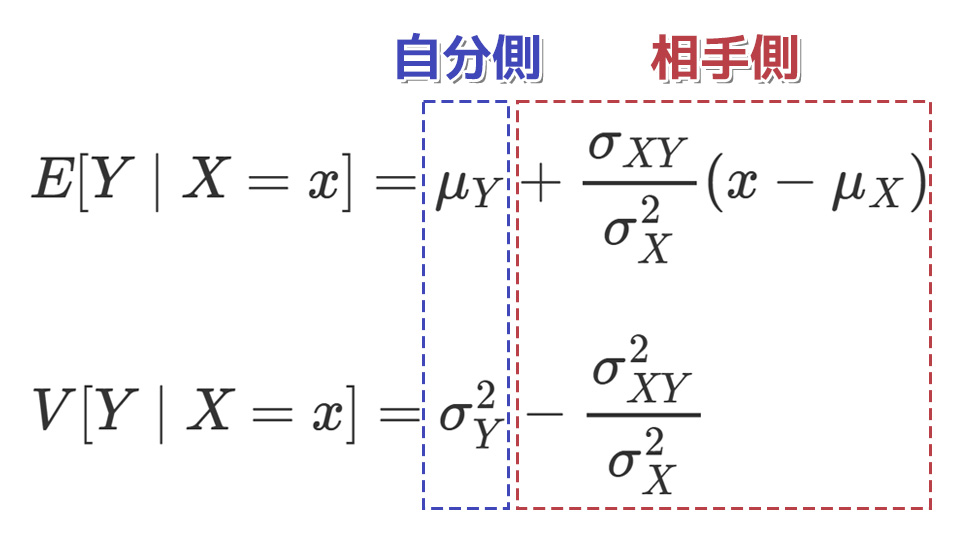
そこで、上のように自分側(第1項)と相手側(第2項)に分けて考えるとイメージしやすく記憶に残りやすいと思います。
まず期待値
\[E[Y \mid X = x] = \mu_Y + \frac{\sigma_{XY}}{\sigma_X^2}(x - \mu_X)\]
についてですが、自分側は単に自身の期待値なので\(\mu_Y\)です。
そこに、相手の影響が関わってきます。はじめに\((x - \mu_X)\)ですが、こちらは偏差(平均からの差)で、どれだけ相手が偏っているかを示すパラメータです。点数が高いほど、この中身は大きくなります。
次に共分散\(\sigma_{XY}\)ですが、こちらは相関の度合いと考えるのが良いです。共分散が0ならいくら\((x - \mu_X)\)が大きくても、影響しなくなります。
最後に\(1/\sigma_X^{2}\)ですが、こちらはスケーリングの役割があります。
これまで偏差\((x - \mu_X)\)(1次元)と共分散\(\sigma_{XY}\)(2次元)を掛けて3次元になっていたので、分散\(\sigma_X^{2}\)(2次元)で割ることで1次元(つまり点数)にしています。
第2項は相手の影響だったので、相手の分散で割ることになります。忘れやすいですが、自分の分散ではありません。
次に条件付き分散
\[V[Y \mid X = x] = \sigma_Y^2 - \frac{\sigma_{XY}^2}{\sigma_X^2}\]
を見ていきます。自分側は先ほど同様に自身の分散なので\(\sigma_Y^2\)です。
続いて相手側(第2項)ですが、期待値の場合と違って第2項は「差」になることを忘れないようにしましょう。相手の情報を知ることで、自分の不確かさが一部減るイメージです。
第2項の\(\sigma_{XY}^2\)は共分散を2乗したものしたものですが、相手とのつながりが強いほど、自分の情報を多く削ることができます。
\(1/\sigma_X^2\)は先ほど同様スケーリングです。別のイメージとして、\(\sigma_X^2\)が大きいほど相手が不安定なので、そこまで自分の分散は減りません。
多変量正規分布への拡張
先ほども記載しましたが、多変量正規分布(k次元)の確率密度関数は以下の通りでした。
\[f(\boldsymbol{x})=\frac{1}{(2\pi)^{k/2}|\boldsymbol{\Sigma}|^{1/2}} \exp\!\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathsf{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right)\]
2変量と比べて計算量は増えますが、大きく変わることはありません。
覚えておきたいのは条件付き期待値・分散で、多変量の場合は行列を使った表記に変わります。
ここで、自分側(求める側)を\(X_1\)、相手側(条件付ける側)を\(X_1\)とし、分散共分散行列\(\Sigma\)は次のように分けて表現します。
\[ \Sigma = \begin{pmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{pmatrix} \]
このとき、\(X_2=x_2\)と条件付けた\(X_1\)の条件付き期待値・分散は次のように表されます。
\[ E[X_1 \mid X_2 = x_2] = \mu_1 + \Sigma_{12} \Sigma_{22}^{-1} (x_2 - \mu_2) \]
\[ V[X_1 \mid X_2 = x_2] = \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} \]
2変量のときと同様で、自分側と相手側に分けて考えれば覚えやすいと思います。
さらに、2項目の\(\Sigma_{12} \Sigma_{22}^{-1}\)が共通なのが嬉しいポイントです。
先ほどの2変量の例では(x,yが逆で気持ち悪いですが)、そのまま
\[ \Sigma = \begin{pmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{pmatrix} = \begin{pmatrix} \sigma_Y^2 & \sigma_{XY} \\ \sigma_{XY} & \sigma_X^2 \end{pmatrix} \]
となるので
\[ E[X_1 \mid X_2 = x_2] = \mu_1 + \Sigma_{12} \Sigma_{22}^{-1} (x_2 - \mu_2) \\ = \mu_Y + \frac{\sigma_{XY}}{\sigma_X^2}(x - \mu_X) \]
\[ V[X_1 \mid X_2 = x_2] = \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} \\ = \sigma_Y^2 - \frac{\sigma_{XY}^2}{\sigma_X^2} \]
と2変量の公式と同じ形になりました。どちらか一方を覚えておけばもう片方も簡易に導けると思います。
では3変量の出題に備えて例題を解きながら確認していきます。
問
数学\((x)\)、物理\((y)\)、地理\((z)\)の試験の点数の平均、分散・共分散は以下の3変量正規分布に従う。
\[ \boldsymbol{\mu} = \begin{pmatrix}\mu_x\\\mu_y\\\mu_z\end{pmatrix} = \begin{pmatrix}70\\50\\50\end{pmatrix} \]
\[ \boldsymbol{\Sigma} = \begin{pmatrix} \sigma_{x}^2 & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{y}^2 & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{z}^2 \end{pmatrix} = \begin{pmatrix} 10^2 & 9^2 & 5^2\\ 9^2 & 12^2 & 4^2\\ 5^2 & 4^2 & 8^2 \end{pmatrix} \]
ここで、物理が40点\((y=40)\)、物理が60点\((z=60)\)だった生徒の、数学の点数\((x)\)の条件付き期待値・分散を求めよ。
地理は文系科目なので、共分散(相関係数)は理系科目同士よりも小さく設定してみました。
まず、分散共分散行列は以下のように分けて考えるのでした。
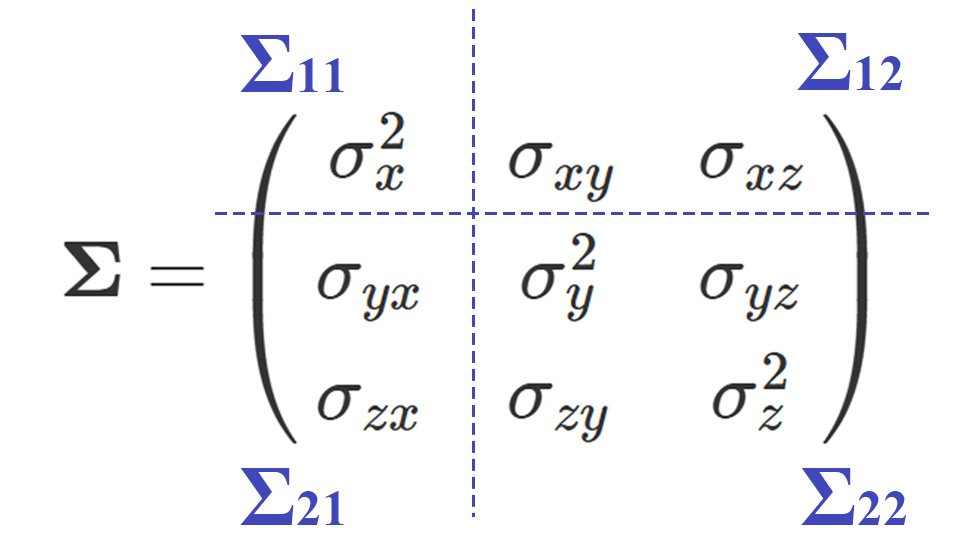
よって、公式より
\[ \begin{align} &E[X \mid Y=40,Z=60] \\ &= \mu_1 + \Sigma_{12} \Sigma_{22}^{-1} (\boldsymbol{x_2} - \boldsymbol{\mu_2}) \\ &=\mu_X + \begin{pmatrix}\sigma_{xy} & \sigma_{xz}\end{pmatrix} \begin{pmatrix} \sigma_{y}^2 & \sigma_{yz} \\ \sigma_{zy} & \sigma_{z}^2 \end{pmatrix}^{-1} \begin{pmatrix} y - \mu_Y \\ z - \mu_Z \end{pmatrix} \\ &=70 + \begin{pmatrix}81 & 25\end{pmatrix} \begin{pmatrix} 144 & 16 \\ 16 & 64 \end{pmatrix}^{-1} \begin{pmatrix} 40 - 50 \\[4pt] 60 - 50 \end{pmatrix} \\ &\approx67.23 \end{align} \]
\[ \begin{align} &V[X \mid Y=40,Z=60] \\ &=\Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} \\ &=\sigma_x^2 - \begin{pmatrix}\sigma_{xy} & \sigma_{xz}\end{pmatrix} \begin{pmatrix} \sigma_{y}^2 & \sigma_{yz} \\ \sigma_{zy} & \sigma_{z}^2 \end{pmatrix}^{-1} \begin{pmatrix}\sigma_{yx}\\ \sigma_{zx}\end{pmatrix} \\ &=100 - \begin{pmatrix}81 & 25\end{pmatrix} \begin{pmatrix} 144 & 16 \\ 16 & 64 \end{pmatrix}^{-1} \begin{pmatrix}81\\[4pt]25\end{pmatrix} \\ &\approx50.32 \end{align} \]
平均点よりも物理が10点低くて地理が10点高い生徒でしたが、理系科目の物理に引っ張られて数学の期待値は平均点よりも低い結果となりました。
まとめ
本記事で紹介した確率密度関数、公式をまとめます。
多変量正規分布の確率密度関数(k次元)
\[f(\boldsymbol{x})=\frac{1}{(2\pi)^{k/2}|\boldsymbol{\Sigma}|^{1/2}} \exp\!\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathsf{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right)\]
2変量正規分布の条件付き期待値・分散
\[ E[Y \mid X = x] = \mu_Y + \frac{\sigma_{XY}}{\sigma_X^2}(x - \mu_X) \]
\[ V[Y \mid X = x] = \sigma_Y^2 - \frac{\sigma_{XY}^2}{\sigma_X^2} \]
多変量正規分布の条件付き期待値・分散
\[ E[X_1 \mid X_2 = x_2] = \mu_1 + \Sigma_{12} \Sigma_{22}^{-1} (x_2 - \mu_2) \]
\[ V[X_1 \mid X_2 = x_2] = \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} \]