【統計準1級】切断正規分布の期待値・分散の導出

統計準1級の範囲表には明確に記載されてはいませんが、連続型分布から切断正規分布が出題される可能性があります。
2級の知識があれば計算自体はできますが、初見では解法に戸惑い、意外と時間がかかる可能性があります。
本記事では切断正規分布の期待値の計算方法と公式を、例題を通して解説していきます。
切断正規分布とは
切断正規分布とは、正規分布のうち、ある範囲に限定された部分だけが観測される分布のことを指します。
例として、あるテストの点数が\(X \sim \mathcal{N}(\mu, \sigma^2)\)に従うことを考えます。
しかし、採点システムが故障してしまい、\(a\)点〜\(b\)点の区間しか観測できなかったとします。
つまり、もともとの正規分布はそのままですが、観測可能な範囲は\(a \le X \le b\)に制限されます。
グラフにすると、以下のように正規分布の左右の裾が\(a\)点、\(b\)点で切り取られたような形になります。
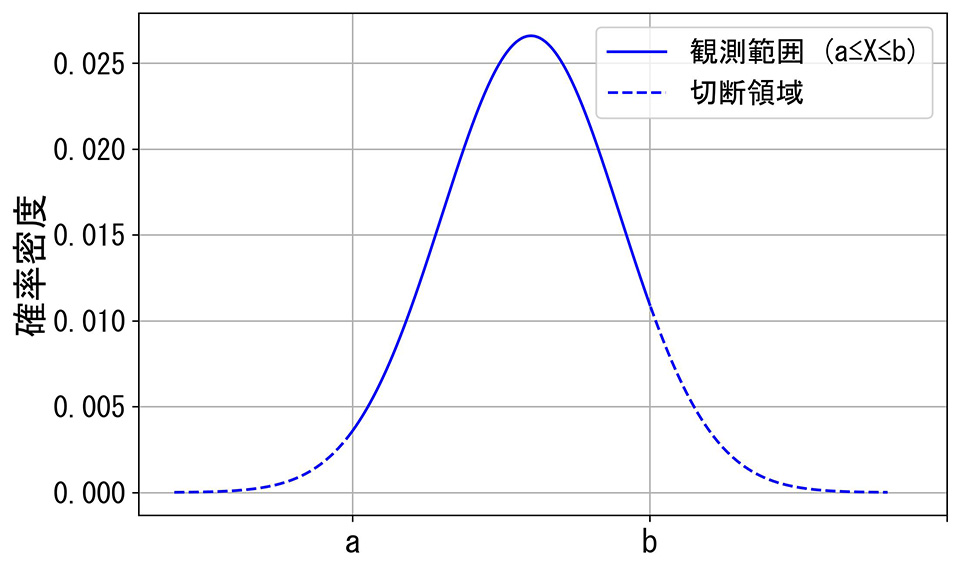
この切断正規分布における期待値は、以下の式で求めることができます。
\[ E[X\mid a\le X\le b] = \mu + \sigma\, \frac{\phi(\alpha)-\phi(\beta)}{\Phi(\beta)-\Phi(\alpha)} \]
ただし、
\[ \alpha = \frac{a-\mu}{\sigma},\qquad \beta = \frac{b-\mu}{\sigma} \]
- \(\phi(x)\):標準正規分布の確率密度関数
- \(\Phi(x)\):標準正規分布の累積分布関数
\(a,b\)を標準化して\(α,β\)とし、\(\phi(x),\Phi(x)\)を含む式に代入しています。
初見では何がなんだか分からないかもしれないので、簡単な例題を通してイメージできるようにしていこうと思います。
例題と公式の導出
問
あるテストの点数が\(X \sim \mathcal{N}(60, 10^2)\)に従うとする。
採点システムの故障により50点〜80点の間しか観測できなかったとき、その期待値を求めよ。
採点システムが故障していない場合、テストの点数が従う分布は
\[ \begin{align} &f(x) = \frac{1}{\sqrt{2\pi}\,10}\, \exp\!\left( -\frac{(x-60)^2}{2\cdot 10^2} \right) \\ &(-\infty < x < \infty) \end{align} \]
となります。
ただし、元の正規分布のまま範囲を\(50 < x < 80\)に限定してしまうと、区間より外側の部分が切断されるため、積分しても1とはなりません。
切断されても確率密度関数の形状自体は変わらないため、係数を掛けることでスケーリングを行います。
そのために、まず元の正規分布において、区間 \(50 < x < 80\) に含まれる確率(積分値)を求めます。
\(a=50, b=80\)を標準化して\(α, β\)とすると
\[ \alpha = \frac{50-60}{10}=-1,\qquad \beta = \frac{80-60}{10}=2 \]
標準正規分布表より、
\[ \begin{align} &P(50 < X < 80) \\ &= \Phi(\beta) - \Phi(\alpha) \\ &= \Phi(2) - \Phi(-1) \\ &= 0.9772-0.1587 \\ &\approx 0.819 \end{align} \]
となります。
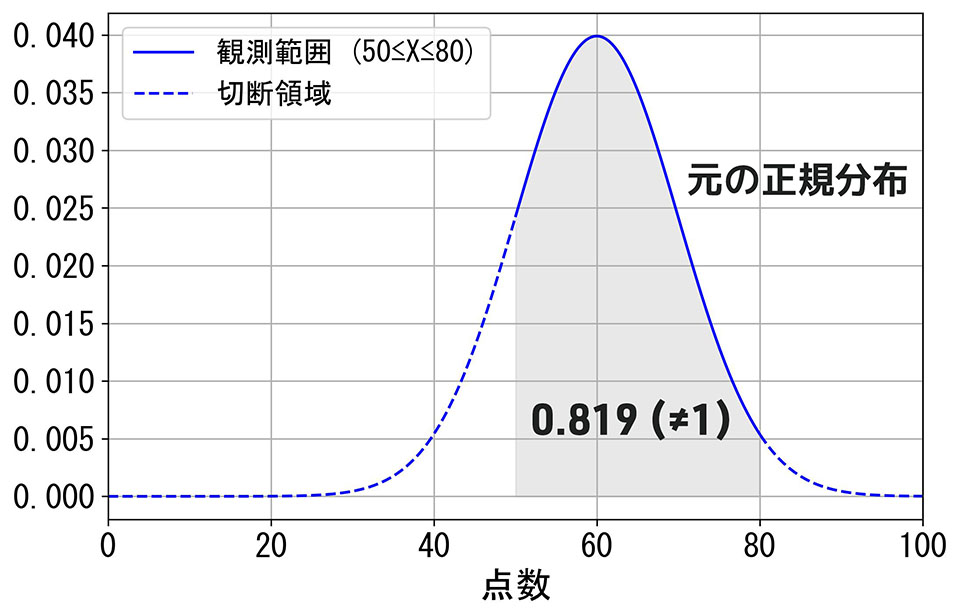
つまり、上のグラフのように元の正規分布の確率密度関数のままだと、積分値は0.819(\(\Phi(\beta)\) - \(\Phi(\alpha)\))になってしまいます。
なので元の正規分布を0.819で割ることで積分値が1となるようにスケーリングしたものが、今回の切断正規分布の確率密度関数\(f_{T}(x)\)になります。
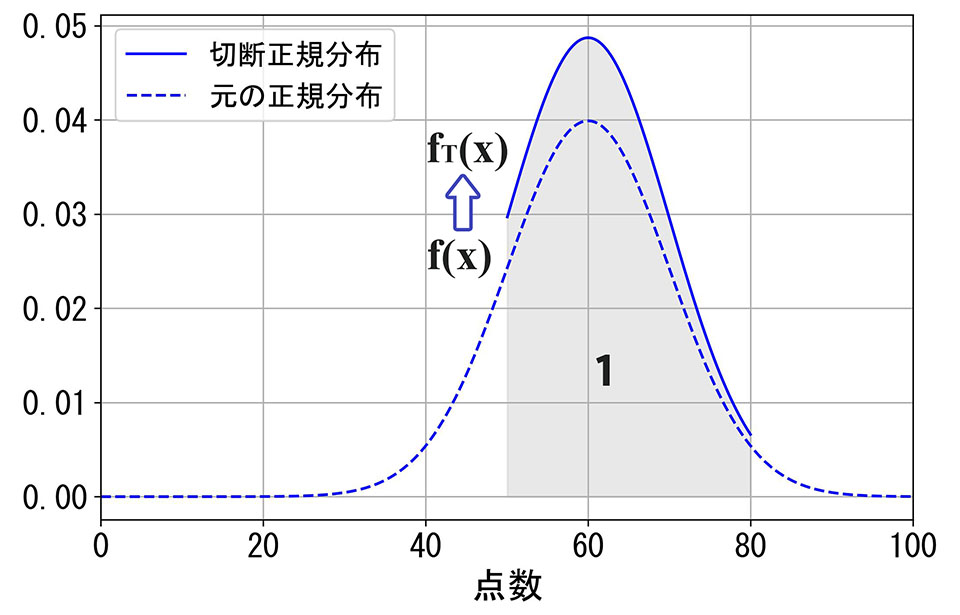
\[ \begin{align} &f_{T}(x) \\ &=\frac{f(x)}{\Phi(2)-\Phi(-1)} \\ &=\frac{1}{\Phi(2)-\Phi(-1)}\frac{1}{\sqrt{2\pi}\,10}\exp\!\left(-\frac{(x-60)^2}{2\cdot 10^2}\right) \\[4pt] &(50<x<80) \end{align} \]
(今後の計算のため、0.819ではなく\(\Phi(\cdot)\)を使った形式で書いています。)
よって期待値を求める式は、
\[ \begin{align} &\int_{50}^{80} x \cdot f_{T}(x)\ dx\\ &=\frac{1}{\Phi(2)-\Phi(-1)}\int_{50}^{80} x \cdot \frac{1}{\sqrt{2\pi}\,10} \exp\!\left(-\frac{(x-60)^2}{2\cdot 10^2}\right)\,dx \end{align} \]
このままでは計算しづらいので、高校数学で習った置換積分を行います。
このような場合は標準正規分布の形にすることが正攻法なので、\(x\)を標準化して\(z\)に置換することを考えます。
\[ z=\frac{x-60}{10} \quad\Longrightarrow\quad dx=10\,dz \]
置換後の積分区間は
\[-1<z<2\ (\alpha<z<\beta)\]
となるため、先ほどの期待値を求める式は
\[ \begin{align} &\int_{50}^{80} x \cdot f_{T}(x)\ dx \\ &=\int_{-1}^{2} (60+10z) \cdot f_{T}(z)\ 10dz \\ &=\frac{1}{\Phi(2)-\Phi(-1)}\int_{-1}^{2} (60+10z) \cdot \frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{z^2}{2}\right)\,dz \\ &=\frac{1}{\Phi(2)-\Phi(-1)}\int_{-1}^{2} (60+10z) \cdot \phi(z)\ dz \end{align} \]
となります。ここで
\[\int \phi(z) = \Phi(z)\]
\[\int z \cdot \phi(z) = -\phi(z)\]
なので、上の式は
\[ \begin{align} &\frac{1}{\Phi(2)-\Phi(-1)} \int_{-1}^{2} (60+10z) \cdot \phi(z)\,dz \\ &=\frac{1}{\Phi(2)-\Phi(-1)} \left[ 60\left(\Phi(2)-\Phi(-1)\right) + 10 \left(-\phi(2)+\phi(-1)\right) \right] \\ &= 60 + \frac{10\bigl(\phi(-1)-\phi(2)\bigr)}{\Phi(2)-\Phi(-1)} \\ &= 60 + \frac{10(0.2420-0.0540)}{0.9772-0.1587} \\ &\approx 62.3 \end{align} \]
と計算できました。記事の最初に示したように、切断正規分布の期待値の公式は、
\[ E[X\mid a\le X\le b] = \mu + \sigma\, \frac{\phi(\alpha)-\phi(\beta)}{\Phi(\beta)-\Phi(\alpha)} \]
でした。比較してみると、各パラメーターが対応していることが分かると思います。
切断正規分布の期待値のイメージは、まず元の期待値\(\mu\)(1項目)から始まり、2項目で切断の影響を補正しています。
2項目は分母でスケーリングを行い、分子で確率密度が高い方に引っ張られるように調整しています。
さらに、この補正全体に\(\sigma\)が掛かることで、元の分布のばらつきの大きさに応じて補正の幅も変わります。
分母と分子の差が逆になっていることと、\(\sigma\)を掛けることさえ覚えておけば、そこまで複雑な公式ではないため簡単に解けると思います。
まとめ
切断正規分布の期待値の公式を、再度記載しておきます。
導出自体はそこまで難しくはないですが、複雑な式ではないためイメージを持って覚えてしまうことをおすすめします。
切断正規分布の期待値
\[ E[X\mid a\le X\le b] = \mu + \sigma\, \frac{\phi(\alpha)-\phi(\beta)}{\Phi(\beta)-\Phi(\alpha)} \]
ただし、
\[ \alpha = \frac{a-\mu}{\sigma},\qquad \beta = \frac{b-\mu}{\sigma} \]
- \(\phi(x)\):標準正規分布の確率密度関数
- \(\Phi(x)\):標準正規分布の累積分布関数